| ページ | 行など | 誤 | 正 |
|---|---|---|---|
| v | 下から2行目 | wycfps.f | wycap.f |
| 6 | 7行目 | より小数の | より少数の |
| 6 | 17行目 | ±π/4 | ±π/2 |
| 9 | 11行 | 同様に15番は | 同様に17番は |
| 12 | 表2.3のD3dの2行目 | (15-17) | (15,17) |
| 13 | 表2.4のC4h | 1.4.(21,24),25,(45,48) | 1,4,21,24,25,28,45,48 |
| 13 | 表2.4のC4 | 1.4.(21,24) | 1,4,21,24 |
| 13 | 表2.4のS4 | 1.4.(45,48) | 1,4,45,48 |
| 23 | 11行目 | ||
| 33 | 11行目 | 行列表現は | 行列表現を |
| 39 | (3.23)の右辺 |
|
|
| 44 | 7行目 | O(ξ) | O(ξi) |
| 45 | 5 行目の右辺 | 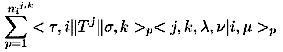 |
|
| 49 | 5行左辺の第3因子 | ||
| 49 | 下から9行目 | ||
| 49 | 下から4行目 | pκ | ρκ |
| 51 | 3行目 | ||
| 63 | (5.6)の1行目 | ||
| 65 | 9行目 | が回映の | が鏡映以外の回映の |
| 76 | 11行目 | 番号で | 番号を |
| 83 | 下から7行目 | 2->z | 3->z |
| 92 | 16行目 | 説明の方が | 説明はこの方が |
| 93 | 14行目 | 一般に斜向軸の | 一般に斜交軸の |
| 96 | 7行目 | 二方格子 | 三方格子 |
| 105 | 9行目 | 点群はすべて | 結晶点群はすべて |
| 153 | 4行目の最後の因子 | exp[iα(k+G)・uα)] | exp[-iα(k+G)・uα] |
| 155 | 12行目 | a*,b*,c* | 2πa*,2πb*,2πc* |
| 155 | 14行目 | Aにはa*を | Aには2πa*を |
| 156 | 3行目 | 直行変換 | 直交変換 |
| 159 | 24行目 | 次の二つは(8.10)は | 次の二つは(8.10)の |
| 162 | 下から10行目 | 原始位置 | 原子位置 |
| 162 | 下から10行目 | をもつ原始 | をもつ原子 |
| 162 | 下から3行目 | Ohは | Ohの |
| 165 | (8.12)の下 | φμ,ν作用して | φμ,νに作用して |
| 167 | プログラム例8.2の7行目のINTEGER KP(2,500),INS(4,100) のあとに ,ND(12) をつける。 | ||
| 198 | プログラム例9.2の8行目の下に | READ(5,*) NKA を追加 | |
| 231 | 1行目から2行目 | この場合はNB,KABCは無視される。 | この場合NBは無視される。 KABC=1にしなければならない。 |
| 234 | RECTAGの表 | RECT(3,p) | RECT(4,p) |
| 234 | RECTAGの表 | 逆格子ベクトルの直交座標 | 逆格子ベクトルの直交座標、第4成分はその大きさ |
| 237 | TSBZEGの表 | REC(3,14) | REC(4,14) |
| 237 | TSBZEGの表 | 上の逆格子ベクトルの直交座標 | 上の逆格子ベクトルの直交座標、 第4成分はその大きさ |
| 238 | TSIREPの表 | IV | IC |
| 243 | EQUIKKの表 | NBB(3) | KBB(3) |
| 244 | CORRESの表 | NBB(3) | KBB(3) |
| 245 | COMPATの表 | NBB(3)o | KBB(3)i |
| 245 | 下から2行目 | CMRTRV | CMPTRV |
| 246 | CMPTRVの表 | NBB(3) | KBB(3) |
| 249 | CALL TSSWDS の下に | 利用するCOMMON変数 /SPW/ および TSSLPW の内部変数 | |
| 250 | TSLCLAの説明の5行目 | A(p)に,KO,U | A(p)に,KP,U |
| 252 | 下から2行目 | TSIRMI 回転行列 | TSRMI 回転行列 |
| 253 | TSRMIの表の下 | r(MA,MB;J) | r(MA,MB;L) |
| 257 | 面心立方格子のQ | Q(1/2+ξ 1/2 1-ξ) | Q(1/2+ξ 1/2 1/2-ξ) |
| 258 | 六方格子のL | L(1/2 0 0) | L(1/2 0 1/2) |
| 282 | シュアーの補題 | Shuur's lemma | Shur's lemma |
P169の下から8行目の『TSLADSの』で始まる5行の文章を次のものに 変えて下さい。
TSLADSの出力の見出しは7個の整数で,最初の数が既約表現の番号IR, 次はいつも1,3番目はJR,4番目は原子の種類番号IAである。5番目はJR で指定されたΛの次元と,IAで指定された種類の原子の単位胞に含まれる数の積 である。つまりこの5番目の数で与えられるだけの (8.11) の型のブロッホ関数が 対称化の対象になる。次の6番目が,得られた対称化関数の数を与えている。 最後の7番目は,6番目の数を既約表現IRの次元で割った数である。つまり, この数は何組みの対称化関数が得られたかを与えている。白く抜けている部分は GIF 画像です。Netscape の"画像を表示"のメニュー で拡大して見れます。
以上の他にデーターファイル generator の218番は Td3 となっていますが, これは Td4 の間違いです。
まだまだ誤りは残っていると思います。この表自身がまちがっているかも知れません 皆様の御協力をお願いします。お気づきの方は下記に e-mail をお願いします。